class: front <!--- Para correr en ATOM - open terminal, abrir R (simplemente, R y enter) - rmarkdown::render('static/docpres/07_interacciones/7interacciones.Rmd', 'xaringan::moon_reader') About macros.js: permite escalar las imágenes como [scale 50%](path to image), hay si que grabar ese archivo js en el directorio. ---> .pull-left[ # Estadística Multivariada ## Juan Carlos Castillo ## Sociología FACSO - UChile ## 1er Sem 2022 ## [.purple[multivariada.netlify.com]](https://multivariada.netlify.com) ] .pull-right[ .right[ <br> ## .purple[Sesión 8: Regresión Logística (1)]  <br> ] ] --- layout: true class: animated, fadeIn --- class: inverse, bottom, right, animated, slideInRight # Contenidos ## 1. Repaso de sesión anterior ## 2. Introducción a regresión logística --- class: roja bottom right slideInRight # 1. Repaso sesión anterior --- # Conceptos centrales - población - muestra - parámetro - estadístico - **error estándar**: permite expresar un rango de variación probable de un parámetro, con un cierto nivel de probabilidad --- # Distribución normal  --- # Inferencia - `\(H_0\)`: hipótesis nula (en general: no hay diferencias en la población) - Establecer un nivel de significación `\(\alpha\)`, convencionalmente 0.05 o inferior para rechazar `\(H_0\)` -> 95% de confianza - Calcular error estándar - Calcular prueba estadística que permita relacionar el error estándar con los niveles de significación --- # Inferencia en regresión - Se calcula el error estándar del `\(\beta\)` - Se divide el `\(\beta\)` por el error estándar -> prueba `\(t\)` - Se compara el `\(t\)` con el `\(t_{crítico}\)` en la tabla de valores `\(t\)`, asociada a un nivel de confianza y grados de libertad `\(n-k-1\)` - Si `\(t\)` > `\(t_{crítico}\)` = se rechaza `\(H_0\)` con una probabilidad de error _p_. --- # Ejemplo: - ver interpretación paso a paso de tabla de regresión en [Práctica 7](https://multivariada.netlify.app/assignment/07-code/) --- class: roja bottom right # Regresión logística (1) ## Para variables dependientes dicotómicas --- ## Variables - discretas (Rango finito de valores): - Dicotómicas - Politómicas - continuas: - Rango (teóricamente) infinito de valores. --- ## Niveles de medición de variables - NOIR: Nominal, Ordinal, Intervalar, Razón .small[ | Tipo | Características | Propiedad de números | Ejemplo| |------------ |----------------------------------------------|--------------- |----------- | | *Nominal* | Uso de números en lugar de palabras | Identidad | Nacionalidad | | *Ordinal* | Números se usan para ordenar series | + ranking | Nivel educacional | | *Intervalar* | Intervalos iguales entre números | + igualdad | Temperatura | | *Razón* | Cero real | + aditividad | Distancia | ] ??? - Nominal: Números empleados como etiquetas (ej. sexo, raza) - Ordinales: Distintas categorías puede sen ordenados en serie. Posición, no distancia. (ej. cargos en una empresa) - Intervalares: Escalas de unidades iguales. Diferencia entre dos número consecuntivos refleja diferencia empírica. (ej. Horas del día) - Razón: caracterizados por la presencia de un cero absoluto. (ej. frecuencias de eventos) --- ## Tipos de datos en relación a escalas de medición. * *Datos categóricos*: pueden ser medidos sólo mediante escalas nominales, u ordinales en caso de orden de rango * *Datos continuos*: - Medidos en escalas intervalares o de razón - Pueden ser transformados a datos categóricos ??? Conversión de continuo a categórico: estatura (cm) a categorías bajo – mediano – alto --- ## Descriptivos según tipo de variable <br> .small[ | | Categórica | Continua | Categ.(y)/Categ.(x) | Cont.(y)/Categ.(x) | |------------- |--------------------------------- |------------------------- |------------------------------------------------ |------------------------------------------ | | **Ejemplo** | **Estatus Ocupacional** | **Ingreso** | **Estatus Ocupacional (Y) / Género (X)** | **Ingreso (Y) / Género (X)** | | Tabla | Frecuencias / porcentajes | Necesidad de recodificar | Tabla de Contingencia | Clasificar Y | | Gráfico | Barras | Histograma / boxplot | Gráfico de barras condicionado | Histograma, box plot condicionado | ] --- ## Análisis estadístico según tipos de variables - Variable dependiente (y) : lo que quiero explicar - Variable independiente (x): lo que me permite explicar la dependiente .small[ | Variable independiente x | Variable dependiente Categórica | Variable dependiente Continua | |-------------------------- |----------------------------------- |-------------------------------------- | | Categórica | Análisis de tabla de Contigencia, Chi2 | Análisis de Varianza ANOVA, Prueba T | | Continua | Regresión Logística | Correlación / Regresión Lineal | ] ??? --- class: inverse, center, bottom .pull-left[  ] ## ¿Se puede anticipar el final? ??? Si vas al cine a ver esta película, y si antes conoces los datos sobre el Titanic, puedes anticipar el final? --- # Titanic data .small[ <div class="container st-container"> <table class="table table-striped table-bordered st-table st-table-striped st-table-bordered st-multiline "> <thead> <tr> <th align="center" class="st-protect-top-border"><strong>No</strong></th> <th align="center" class="st-protect-top-border"><strong>Variable</strong></th> <th align="center" class="st-protect-top-border"><strong>Stats / Values</strong></th> <th align="center" class="st-protect-top-border"><strong>Freqs (% of Valid)</strong></th> <th align="center" class="st-protect-top-border"><strong>Graph</strong></th> <th align="center" class="st-protect-top-border"><strong>Valid</strong></th> <th align="center" class="st-protect-top-border"><strong>Missing</strong></th> </tr> </thead> <tbody> <tr> <td align="center">1</td> <td align="left">survived [factor]</td> <td align="left" style="padding:8;vertical-align:middle"><table style="border-collapse:collapse;border:none;margin:0"><tr style="background-color:transparent"><td style="padding:0;margin:0;border:0" align="left">1. No sobrevive</td></tr><tr style="background-color:transparent"><td style="padding:0;margin:0;border:0" align="left">2. Sobrevive</td></tr></table></td> <td align="left" style="padding:0;vertical-align:middle"><table style="border-collapse:collapse;border:none;margin:0"><tr style="background-color:transparent"><td style="padding:0 5px 0 7px;margin:0;border:0" align="right">619</td><td style="padding:0 2px 0 0;border:0;" align="left">(</td><td style="padding:0;border:0" align="right">59.2%</td><td style="padding:0 4px 0 2px;border:0" align="left">)</td></tr><tr style="background-color:transparent"><td style="padding:0 5px 0 7px;margin:0;border:0" align="right">427</td><td style="padding:0 2px 0 0;border:0;" align="left">(</td><td style="padding:0;border:0" align="right">40.8%</td><td style="padding:0 4px 0 2px;border:0" align="left">)</td></tr></table></td> <td align="left" style="vertical-align:middle;padding:0;background-color:transparent;"><img style="border:none;background-color:transparent;padding:0;max-width:max-content;" src="data:image/png;base64, iVBORw0KGgoAAAANSUhEUgAAAGUAAAA3BAMAAADnFJkAAAAABGdBTUEAALGPC/xhBQAAACBjSFJNAAB6JgAAgIQAAPoAAACA6AAAdTAAAOpgAAA6mAAAF3CculE8AAAAD1BMVEX////9/v2mpqbw8PD///+xh0SBAAAAAnRSTlMAAHaTzTgAAAABYktHRACIBR1IAAAAB3RJTUUH5gcHEx01lIEDgAAAAD9JREFUSMdjYBh+QIkEoADVo2xMPBjVM6pnVM/w1kNOGSJIAhCgsx4CXsCqB3+4GY3qGdUzqmcE6SGnDBlOAADPUVxOmytYlQAAACV0RVh0ZGF0ZTpjcmVhdGUAMjAyMi0wNy0wN1QxOToyOTo1MyswMDowMFLgsSAAAAAldEVYdGRhdGU6bW9kaWZ5ADIwMjItMDctMDdUMTk6Mjk6NTMrMDA6MDAjvQmcAAAAAElFTkSuQmCC"></td> <td align="center">1046 (100.0%)</td> <td align="center">0 (0.0%)</td> </tr> <tr> <td align="center">2</td> <td align="left">sex [factor]</td> <td align="left" style="padding:8;vertical-align:middle"><table style="border-collapse:collapse;border:none;margin:0"><tr style="background-color:transparent"><td style="padding:0;margin:0;border:0" align="left">1. Hombre</td></tr><tr style="background-color:transparent"><td style="padding:0;margin:0;border:0" align="left">2. Mujer</td></tr></table></td> <td align="left" style="padding:0;vertical-align:middle"><table style="border-collapse:collapse;border:none;margin:0"><tr style="background-color:transparent"><td style="padding:0 5px 0 7px;margin:0;border:0" align="right">658</td><td style="padding:0 2px 0 0;border:0;" align="left">(</td><td style="padding:0;border:0" align="right">62.9%</td><td style="padding:0 4px 0 2px;border:0" align="left">)</td></tr><tr style="background-color:transparent"><td style="padding:0 5px 0 7px;margin:0;border:0" align="right">388</td><td style="padding:0 2px 0 0;border:0;" align="left">(</td><td style="padding:0;border:0" align="right">37.1%</td><td style="padding:0 4px 0 2px;border:0" align="left">)</td></tr></table></td> <td align="left" style="vertical-align:middle;padding:0;background-color:transparent;"><img style="border:none;background-color:transparent;padding:0;max-width:max-content;" src="data:image/png;base64, iVBORw0KGgoAAAANSUhEUgAAAGsAAAA3BAMAAAD53amzAAAABGdBTUEAALGPC/xhBQAAACBjSFJNAAB6JgAAgIQAAPoAAACA6AAAdTAAAOpgAAA6mAAAF3CculE8AAAAD1BMVEX////9/v2mpqbw8PD///+xh0SBAAAAAnRSTlMAAHaTzTgAAAABYktHRACIBR1IAAAAB3RJTUUH5gcHEx01lIEDgAAAAEJJREFUSMdjYBjeQIk0oADVpmxMEhjVNqptVNuoNqzayCyCBEkDAgOiDZ9H8GjDE5JGo9pGtY1qG9VGrDYyi6DhCgCNyWWr8oQgJAAAACV0RVh0ZGF0ZTpjcmVhdGUAMjAyMi0wNy0wN1QxOToyOTo1MyswMDowMFLgsSAAAAAldEVYdGRhdGU6bW9kaWZ5ADIwMjItMDctMDdUMTk6Mjk6NTMrMDA6MDAjvQmcAAAAAElFTkSuQmCC"></td> <td align="center">1046 (100.0%)</td> <td align="center">0 (0.0%)</td> </tr> <tr> <td align="center">3</td> <td align="left">age [numeric]</td> <td align="left" style="padding:8;vertical-align:middle"><table style="border-collapse:collapse;border:none;margin:0"><tr style="background-color:transparent"><td style="padding:0;margin:0;border:0" align="left">Mean (sd) : 29.9 (14.4)</td></tr><tr style="background-color:transparent"><td style="padding:0;margin:0;border:0" align="left">min ≤ med ≤ max:</td></tr><tr style="background-color:transparent"><td style="padding:0;margin:0;border:0" align="left">0.2 ≤ 28 ≤ 80</td></tr><tr style="background-color:transparent"><td style="padding:0;margin:0;border:0" align="left">IQR (CV) : 18 (0.5)</td></tr></table></td> <td align="left" style="vertical-align:middle">98 distinct values</td> <td align="left" style="vertical-align:middle;padding:0;background-color:transparent;"><img style="border:none;background-color:transparent;padding:0;max-width:max-content;" src="data:image/png;base64, iVBORw0KGgoAAAANSUhEUgAAAJgAAABuBAMAAAApJ8cWAAAABGdBTUEAALGPC/xhBQAAACBjSFJNAAB6JgAAgIQAAPoAAACA6AAAdTAAAOpgAAA6mAAAF3CculE8AAAAD1BMVEX////9/v2mpqbw8PD///+xh0SBAAAAAnRSTlMAAHaTzTgAAAABYktHRACIBR1IAAAAB3RJTUUH5gcHEx01lIEDgAAAALtJREFUaN7t1+ENgyAQhmFWoBtINyj776YQSbQtcoen0fb9/pHoIyFwh86Rnvj3PMKUwetSxeIUMDAwMB2mLUOb2FM5OzAwMLCLYakmBissGS8wsDOxvIOtsDwAA/tvTHikZJhwdmBgYDJM8Ccrx2K7I4MdjTVuMTqs0RBmbPXJvdjqKTCwX8Pq57MDq8/uMKy0DBOsVCwzbPn+Wdj3JtqJlRUJVtjnDgYDuwMW5gwWWBlkcXlx2R1HejIC7qcE36kYv9kAAAAldEVYdGRhdGU6Y3JlYXRlADIwMjItMDctMDdUMTk6Mjk6NTMrMDA6MDBS4LEgAAAAJXRFWHRkYXRlOm1vZGlmeQAyMDIyLTA3LTA3VDE5OjI5OjUzKzAwOjAwI70JnAAAAABJRU5ErkJggg=="></td> <td align="center">1046 (100.0%)</td> <td align="center">0 (0.0%)</td> </tr> </tbody> </table> <p>Generated by <a href='https://github.com/dcomtois/summarytools'>summarytools</a> 1.0.0 (<a href='https://www.r-project.org/'>R</a> version 4.1.3)<br/>2022-07-07</p> </div> ] --- # Sobrevivientes .pull-left[ .small[ ```r plot1 <-ggplot(tt, aes(survived, fill=survived)) + geom_bar() + geom_text( aes(label = scales::percent((..count..)/sum(..count..))), stat='count',size=10, vjust = 3) + theme(legend.position="none", text = element_text(size = 30), axis.title=element_blank()) ``` ] ] .pull-right[ <!-- --> ] --- # Sexo .center[ <!-- --> ] --- ## Sobrevivencia / sexo .pull-left[  ] .pull-right[ .medium[ ``` ## ## Hombre Mujer ## No sobrevive 0.79 0.25 ## Sobrevive 0.21 0.75 ``` El 75% de las mujeres sobrevive, mientras el 25% no sobrevive. ] ] --- class: inverse, middle, center ## ¿En qué medida la probabilidad de sobrevivir depende del sexo? ## ¿Es esta probabilidad estadísticamente significativa? --- # Alternativas: - tabla de contingencia, `\(\chi^2\)` - análisis de tendencia general, significación estadística - pero ... poco parsimoniosa, y no hay control estadístico - ¿Aprovechar las ventajas del modelo de regresión? - expresar la relación en un número ( `\(\beta\)` ) - inferencia - control estadístico --- # Regresión ### Modelando la probabilidad de sobrevivir con regresión OLS .small[ ```r reg_tit=lm(survived ~ sex, data= tt) ``` ``` ## Warning in model.response(mf, "numeric"): using type = "numeric" with a factor ## response will be ignored ``` ``` ## Warning in Ops.factor(y, z$residuals): '-' not meaningful for factors ``` ] -> Advertencia de R --- ## Modelo de probabilidad lineal .pull-left[ .small[ Se da este nombre a los modelos de regresión donde una variable dependiente dicotómica se estima de manera tradicional (mínimos cuadrados ordinarios) ```r str(tt$survived) ``` ``` ## Factor w/ 2 levels "No sobrevive",..: 2 2 1 1 1 2 2 1 2 1 ... ``` ```r tt <- tt %>% mutate(survived_n=recode(survived, "No sobrevive"=0, "Sobrevive"=1)) str(tt$survived_n) ``` ``` ## num [1:1046] 1 1 0 0 0 1 1 0 1 0 ... ``` ] ] .pull-right[ .small[ ```r reg_tit=lm(survived_n ~ sex, data=tt) ``` <table style="border-collapse:collapse; border:none;"> <tr> <th style="border-top: double; text-align:center; font-style:normal; font-weight:bold; padding:0.2cm; text-align:left; ">&nbsp;</th> <th colspan="2" style="border-top: double; text-align:center; font-style:normal; font-weight:bold; padding:0.2cm; ">Modelo 1</th> </tr> <tr> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; text-align:left; ">Predictores</td> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; ">&szlig;</td> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; ">std. Error</td> </tr> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; ">(Intercept)</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">0.205 ^***</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">0.016</td> </tr> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; ">sex [Mujer]</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">0.547 ^***</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">0.027</td> </tr> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; padding-top:0.1cm; padding-bottom:0.1cm; border-top:1px solid;">Observations</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left; border-top:1px solid;" colspan="2">1046</td> </tr> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; padding-top:0.1cm; padding-bottom:0.1cm;">R² / R² adjusted</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left;" colspan="2">0.289 / 0.289</td> </tr> <tr> <td colspan="3" style="font-style:italic; border-top:double black; text-align:right;">* p&lt;0.05&nbsp;&nbsp;&nbsp;** p&lt;0.01&nbsp;&nbsp;&nbsp;*** p&lt;0.001</td> </tr> </table> ] ] --- ## Significado coeficientes modelo probabilidad lineal .pull-left[ **Promedio de supervivencia por sexo** <!-- html table generated in R 4.1.3 by xtable 1.8-4 package --> <!-- Thu Jul 07 15:29:54 2022 --> <table border=1> <tr> <th> </th> <th> Mean </th> <th> N </th> <th> Std. Dev. </th> </tr> <tr> <td> Hombre </td> <td align="right"> 0.21 </td> <td align="right"> 658 </td> <td align="right"> 0.40 </td> </tr> <tr> <td> Mujer </td> <td align="right"> 0.75 </td> <td align="right"> 388 </td> <td align="right"> 0.43 </td> </tr> <tr> <td> Total </td> <td align="right"> 0.41 </td> <td align="right"> 1046 </td> <td align="right"> 0.49 </td> </tr> </table> ] .pull-right[ - El valor del intercepto=0.205 (0.21 aproximado) es el valor predicho para la categoría de referencia "hombre". - El `\(\beta\)` de sexo (mujer) =0.547 sumado al intercepto equivale al porcentaje de supervivencia de mujeres] --- class: roja, middle # funciona ... .yellow[PERO] --- ## Limitaciones modelo de regresión lineal para dependientes dicotómicas .center[ <!-- --> ] --- ## Problemas .... .center[ <!-- --> ] --- # Problemas ... .pull-left[ Si hubieran sobrevivido todos los menores de 20 y muerto todos los mayores de 40 ... ] .pull-right[ <!-- --> ] --- class: inverse ## Problemas regresión tradicional (OLS) para dependientes dicotómicas - ### Eventuales predicciones fuera del rango de probabilidades posibles - ### Ajuste a los datos / residuos: ¿Es la mejor aproximación una recta? --- class: roja, right ## La regresión .yellow[logística] ofrece una solución a los problemas del rango de predicciones y de ajuste a los datos del modelo de probabilidad lineal -- ## Se logra mediante una _transformación_ de lo(s) beta(s) a .yellow[coeficientes *LOGIT*] ] --- class: middle center  --- ## OLS vs Logit .pull-left[ <!-- --> ] .pull-right[ 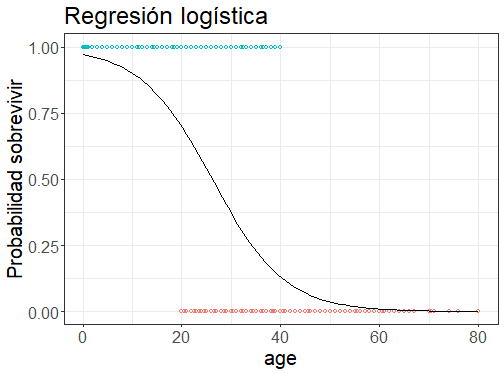<!-- --> ] --- # ¿Qué es el logit? -- ## Es el logaritmo de los odds -- # ... qué son los odds? -- ## Una razón de *probabilidades* -- ## Para llegar hasta regresión logística, hay que pasar por los odds (chances), y los odds-ratio (proporción de chances) --- # Odds - **odds** (chances): probabilidad de que algo ocurra dividido por la probabilidad de que no ocurra `$$Odds=\frac{p}{1-p}$$` -- .medium[ Ej. Titanic: - 427 sobrevivientes (41%), 619 muertos (59%) `$$Odds_{sobrevivir}=427/619=0.41/0.59=0.69$$` **Es decir, las chances de sobrevivir son de 0.69**] --- # Odds - Odds de 1 significan chances iguales, menores a 1 son negativas y mayores a 1 son positivas - _Propiedad simétrica_: - un `\(Odd=4\)` es una asociación positiva proporcional a la asociación negativa `\(Odd=1/4=0.25\)` --- .pull-left[ ## Odds de superviviencia para los hombres .medium[ ``` ## ## Hombre Mujer ## No sobrevive 523 96 ## Sobrevive 135 292 ``` ] .medium[ ``` ## ## Hombre Mujer ## No sobrevive 0.79 0.25 ## Sobrevive 0.21 0.75 ``` El 21% de los hombres sobrevive mientras el 79% no sobrevive. ] ] -- .pull-right[ .medium[ `$$Odds_{hombres}=\frac{0.21}{0.79}=0.27$$` *La probabilidad de sobrevivencia en los hombres es 0.27 veces a la no sobrevivencia* ... o en otros términos *Hay 0.27 hombres que sobreviven por cada uno que no sobrevive* *Hay 27 hombres que sobreviven por cada 100 hombres que no sobreviven* ] ] --- ## Odds de superviviencia para las mujeres .pull-left[ .medium[ ``` ## ## Hombre Mujer ## No sobrevive 0.79 0.25 ## Sobrevive 0.21 0.75 ``` El 75% de las mujeres sobrevive, mientras el 25% no sobrevive. ] ] -- .pull-right[ .medium[ `$$Odds_{mujeres}=\frac{0.75}{0.25}=3$$` *La probabilidad de sobrevivencia en las mujeres es 3 veces a la no sobrevivencia* *Hay 3 mujeres que sobreviven por cada mujer que no sobrevive* o en otros términos *Hay 300 mujeres que sobreviven al titanic por cada 100 mujeres que no sobreviven* ] ] --- ## Odds ratio (OR) .pull-left[ - los odds-ratio (o razón de chances) permiten reflejar la asociación entre las chances de dos variables dicotómicas **¿Tienen las mujeres más chances de sobrevivir que los hombres?** ] -- .pull-right[ .medium[ <table style="border-collapse:collapse; border:none;"> <tr> <th style="border-top:double; text-align:center; font-style:italic; font-weight:normal; border-bottom:1px solid;" rowspan="2">survived</th> <th style="border-top:double; text-align:center; font-style:italic; font-weight:normal;" colspan="2">sex</th> <th style="border-top:double; text-align:center; font-style:italic; font-weight:normal; font-weight:bolder; font-style:italic; border-bottom:1px solid; " rowspan="2">Total</th> </tr> <tr> <td style="border-bottom:1px solid; text-align:center; padding:0.2cm;">Hombre</td> <td style="border-bottom:1px solid; text-align:center; padding:0.2cm;">Mujer</td> </tr> <tr> <td style="padding:0.2cm; text-align:left; vertical-align:middle;">No sobrevive</td> <td style="padding:0.2cm; text-align:center; "><span style="color:black;">523</span><br><span style="color:#339933;">79.5&nbsp;&#37;</span></td> <td style="padding:0.2cm; text-align:center; "><span style="color:black;">96</span><br><span style="color:#339933;">24.7&nbsp;&#37;</span></td> <td style="padding:0.2cm; text-align:center; "><span style="color:black;">619</span><br><span style="color:#339933;">59.2&nbsp;&#37;</span></td> </tr> <tr> <td style="padding:0.2cm; text-align:left; vertical-align:middle;">Sobrevive</td> <td style="padding:0.2cm; text-align:center; "><span style="color:black;">135</span><br><span style="color:#339933;">20.5&nbsp;&#37;</span></td> <td style="padding:0.2cm; text-align:center; "><span style="color:black;">292</span><br><span style="color:#339933;">75.3&nbsp;&#37;</span></td> <td style="padding:0.2cm; text-align:center; "><span style="color:black;">427</span><br><span style="color:#339933;">40.8&nbsp;&#37;</span></td> </tr> <tr> <td style="padding:0.2cm; border-bottom:double; font-weight:bolder; font-style:italic; text-align:left; vertical-align:middle;">Total</td> <td style="padding:0.2cm; text-align:center; border-bottom:double;"><span style="color:black;">658</span><br><span style="color:#339933;">100&nbsp;&#37;</span></td> <td style="padding:0.2cm; text-align:center; border-bottom:double;"><span style="color:black;">388</span><br><span style="color:#339933;">100&nbsp;&#37;</span></td> <td style="padding:0.2cm; text-align:center; border-bottom:double;"><span style="color:black;">1046</span><br><span style="color:#339933;">100&nbsp;&#37;</span></td> </tr> </table> ] ] --- # Odds Ratio **¿Cuantas más chances de sobrevivir tienen las mujeres respecto de los hombres?** - OR supervivencia mujeres / OR supervivencia hombres .medium[ `$$OR=\frac{p_{m}/(1-p_{m})}{p_{h}/(1-p_{h})}=\frac{0.753/(1-0.753)}{0.205/(1-0.205)}=\frac{3.032}{0.257}=11.78$$` ] -- ### Las chances de sobrevivir de las mujeres son **11.78** veces más que las de los hombres. --- class: inverse, middle, center ## El Odds-Ratio (OR) nos permite expresar **en un número** la relación entre dos variables categóricas ## Por lo tanto, es una versión del `\(\beta\)` para dependientes categóricas --- class: inverse, middle, center ## Pero ... el **OR** tiene algunas limitaciones que requieren una transformación adicional, tema de la .yellow[próxima clase] --- class: inverse ## Resumen - limitaciones de OLS para dependientes dicotómicas - requiere de ajustes y transformaciones para que la estimación tenga sentido - regresión logística: ajusta el modelo para dependientes dicotómicas - pasa por el cálculo de los odds-ratio, que resumen en 1 número la relación entre dos variables categóricas --- # Siguiente sesión - logit - estimación e interpretación regresión logística - ajuste regresión logística --- class: front .pull-left[ # Estadística Multivariada ## Juan Carlos Castillo ## Sociología FACSO - UChile ## 1er Sem 2022 ## [multivariada.netlify.com](https://multivariada.netlify.com) ] .pull-right[ .right[ <br>  ] ]