class: front <!--- Para correr en ATOM - open terminal, abrir R (simplemente, R y enter) - rmarkdown::render('static/docpres/07_interacciones/7interacciones.Rmd', 'xaringan::moon_reader') About macros.js: permite escalar las imágenes como [scale 50%](path to image), hay si que grabar ese archivo js en el directorio. ---> .pull-left[ # Estadística Multivariada ## Juan Carlos Castillo ## Sociología FACSO - UChile ## 1er Sem 2022 ## [multivariada.netlify.com](https://multivariada.netlify.com) ] .pull-right[ .right[  <br> <br> ## Sesión 10. Primer bloque: Supuestos y robustez del modelo de regresión ] ] --- layout: true class: animated, fadeIn --- class: inverse, middle, center # ¿Qué tan apropiado es el modelo de regresión para dar cuenta de las relaciones entre los datos? --- .center[ 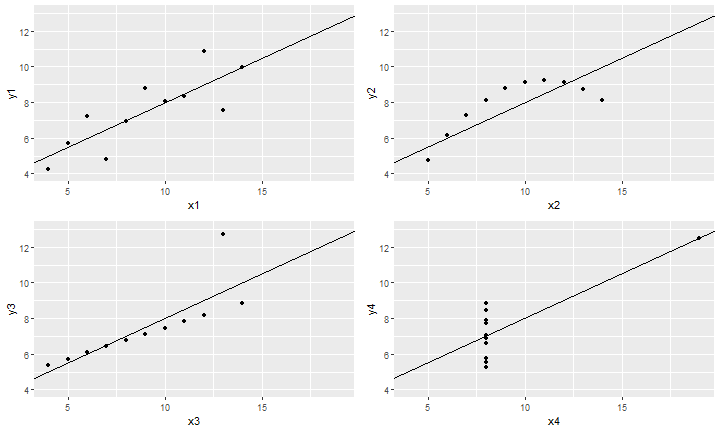<!-- --> ] .small[ Anscombe, F. J. (1973). Graphs in Statistical Analysis. The American Statistician, 27(1), 17–21. https://doi.org/10.1080/00031305.1973.10478966] --- class: middle .tiny[ <table style="border-collapse:collapse; border:none;"> <tr> <th style="border-top: double; text-align:center; font-style:normal; font-weight:bold; padding:0.2cm; text-align:left; ">&nbsp;</th> <th colspan="3" style="border-top: double; text-align:center; font-style:normal; font-weight:bold; padding:0.2cm; ">Modelo 1</th> <th colspan="3" style="border-top: double; text-align:center; font-style:normal; font-weight:bold; padding:0.2cm; ">Modelo 2</th> <th colspan="3" style="border-top: double; text-align:center; font-style:normal; font-weight:bold; padding:0.2cm; ">Modelo 3</th> <th colspan="3" style="border-top: double; text-align:center; font-style:normal; font-weight:bold; padding:0.2cm; ">Modelo 4</th> </tr> <tr> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; text-align:left; ">Predictores</td> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; ">β</td> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; ">std. Error</td> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; ">p</td> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; ">β</td> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; ">std. Error</td> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; col7">p</td> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; col8">β</td> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; col9">std. Error</td> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; 0">p</td> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; 1">β</td> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; 2">std. Error</td> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; 3">p</td> </tr> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; ">(Intercept)</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">3.00 ^*</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">1.12</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "><strong>2.573e&#45;02</strong></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">3.00 ^*</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">1.13</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; col7"><strong>2.576e&#45;02</strong></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; col8">3.00 ^*</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; col9">1.12</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; 0"><strong>2.562e&#45;02</strong></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; 1">3.00 ^*</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; 2">1.12</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; 3"><strong>2.559e&#45;02</strong></td> </tr> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; ">x1</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">0.50 ^**</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">0.12</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "><strong>2.170e&#45;03</strong></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; col7"></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; col8"></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; col9"></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; 0"></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; 1"></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; 2"></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; 3"></td> </tr> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; ">x2</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">0.50 ^**</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">0.12</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; col7"><strong>2.179e&#45;03</strong></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; col8"></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; col9"></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; 0"></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; 1"></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; 2"></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; 3"></td> </tr> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; ">x3</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; col7"></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; col8">0.50 ^**</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; col9">0.12</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; 0"><strong>2.176e&#45;03</strong></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; 1"></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; 2"></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; 3"></td> </tr> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; ">x4</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; col7"></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; col8"></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; col9"></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; 0"></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; 1">0.50 ^**</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; 2">0.12</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; 3"><strong>2.165e&#45;03</strong></td> </tr> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; padding-top:0.1cm; padding-bottom:0.1cm; border-top:1px solid;">Observations</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left; border-top:1px solid;" colspan="3">11</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left; border-top:1px solid;" colspan="3">11</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left; border-top:1px solid;" colspan="3">11</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left; border-top:1px solid;" colspan="3">11</td> </tr> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; padding-top:0.1cm; padding-bottom:0.1cm;">R² / R² adjusted</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left;" colspan="3">0.667 / 0.629</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left;" colspan="3">0.666 / 0.629</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left;" colspan="3">0.666 / 0.629</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left;" colspan="3">0.667 / 0.630</td> </tr> <tr> <td colspan="13" style="font-style:italic; border-top:double black; text-align:right;">* p&lt;0.05&nbsp;&nbsp;&nbsp;** p&lt;0.01&nbsp;&nbsp;&nbsp;*** p&lt;0.001</td> </tr> </table> ] --- class: middle, center  --- class: inverse <br> <br> <br> - El modelo de regresión es para asociaciones **lineales** entre variables -- - En ausencia de asocaciones lineales se pueden generar distorsiones en la estimación -- - El **Análisis de robustez** o **chequeo de supuestos** permite analizar en qué medida el modelo es una representación adecuada de las asociaciones entre las variables. --- class: inverse middle ## **A revisar:** .pull-left-wide[ 1. Observaciones influyentes 2. Linealidad 3. Homogeneidad de varianza (homocedasticidad) 4. Inflación de varianza ] .pull-right-narrow[ <br> <br> <br>  ] --- class: inverse middle ## **A revisar:** .pull-left-wide[ 1. **Observaciones influyentes** 2. Linealidad 3. Homogeneidad de varianza (homocedasticidad) 4. Inflación de varianza ] .pull-right-narrow[ <br> <br> <br>  ] --- class: center .small[ 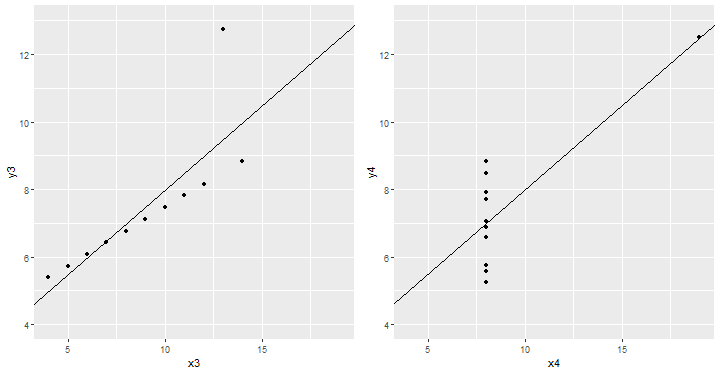<!-- --> ] -- Una observación es **influyente** si su presencia/ausencia genera un cambio importante en la estimación de los coeficientes de regresión --- ## Ouliers vs observaciones influyentes - la identificación descriptiva de un outlier en una variable no necesariamente implica influencia -- .center[ .medium[ .content-box-red[ .red[ **No todo outlier es una observación influyente, pero toda observación influyente es un outlier ** ] ] ] ] -- - la capacidad de influencia de un outlier se asocia al concepto de **"apalancamiento"** (leverage). --- ## Identificando influyentes: Distancia de Cook `$$DCook=\frac{\sum(\hat{y_{j}}-\hat{y_{j(i)}})^2}{p*MSE}$$` Se trata de una diferencia de la predicción del modelo con y sin la observación `\(i\)`, ponderada por el número de parametros en el modelo (p) y la media cuadrática del error (MSE). Se establece un punto de corte de `\(4/(n-k-1)\)`, valores mayores se consideran influyentes -> outliers con alta capacidad de palanca. --- ## Manejo de casos influyentes .pull-left[ .small[ 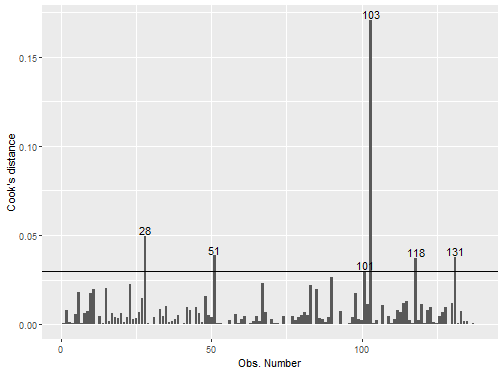<!-- --> ] ] .pull-right[ .content-box-red[ - estimar Cook para todas las observaciones - detectar observaciones con Cook > punto de corte = influyentes - re-estimar modelo sin las observaciones y comparar resultados ] ] --- class: inverse middle ## **A revisar:** .pull-left-wide[ 1. Observaciones influyentes 2. **Linealidad** 3. Homogeneidad de varianza (homocedasticidad) 4. Inflación de varianza ] .pull-right-narrow[ <br> <br> <br>  ] --- ## Linealidad (asociaciones lineales) Recordando: - valores predichos: `\(\hat{Y}\)` - residuos `\(\hat{Y}-Y\)` -- Una forma en que se puede expresar la linealidad se relaciona con la **distribución de los residuos** En presencia de linealidad se esperaría que los residuos se distribuyan **aleatoriamente** en torno a la recta de regresión (representada por los valores predichos) --- ## Predichos (fitted) y residuos en Anscombe .center[ 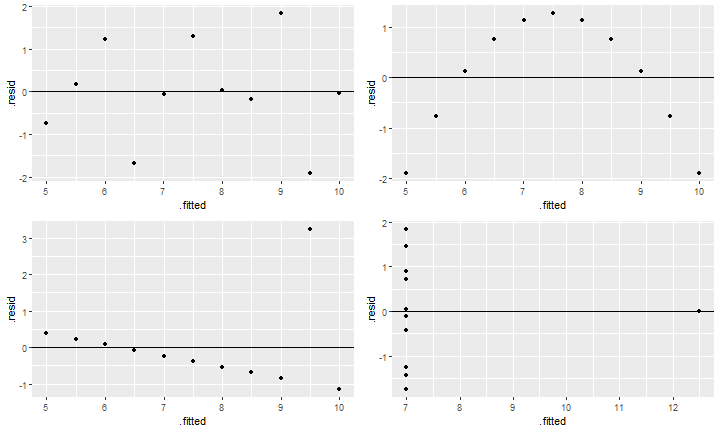<!-- --> ] --- ## Predichos (fitted) y residuos en Anscombe .center[ <!-- --> ] --- ## Interpretación del gráfico de Diagnóstico. - Los residuos deben ser **independientes** de los valores predichos - Cualquier correlación entre los residuos y los valores predichos violarían este supuesto. - Sí los residuos muestran una patrón no lineal, como una **relación curvilinea**, el modelo esta especificado incorrectamente. --- ## ¿Qué hacer en caso de no-linealidad? - descartar observaciones influyentes - transformación de variables, ej: - polinomial - logarítmica --- ## Transformación polinomial .pull-left[ - transformaciones de potencia que permiten capturar asocaciones no lineales / curvas - además de la variable original `\(x\)`, se suma(n) al modelo terminos cuadráticos `\(x^2\)`, cúbicos `\(x^3\)`... - caso típico: edad ] .pull-right[  ] --- ## Transformación polinomial .pull-left[  ] .pull-right[  ] --- ## Transformación logarítmica - utilizada para variables con un alto sesgo en su distribución .center[  ] - pondera crecientemente las diferencias entre los valores de la escala --- ## Transformación logarítmica .pull-left[ - Se reemplaza la variable por la transformada logarítmicamente en el modelo (a diferencia de los polinomios) - caso típico: ingreso ] .pull-right[  ] --- class: inverse middle ## **A revisar:** .pull-left-wide[ 1. Observaciones influyentes 2. Linealidad 3. **Homogeneidad de varianza (homocedasticidad)** 4. Inflación de varianza ] .pull-right-narrow[ <br> <br> <br>  ] --- ## Homogeneidad de varianza - se refiere al supuesto de que la varianza de los residuos debería ser homogenea a lo largo de los valores predichos - problemas de homocedasticidad en los residuos (**=heterocedasticidad**) puede afectar la estimación de los parámetros y su significación estadística --- ## Homogeneidad de varianza .center[  ] --- ## Detección de Heterocedasticidad - test Breush-Pagan, en R: `car::ncvTest(model1)` - test de Cook-Weisberg, en R: `lmtest::bptest(model1)` - se contrasta la hipótesis nula de que la varianza del error es constante (=no diferencias), y la hipótesis alternativa de que el error de la varianza no es constante. - por lo tanto, se busca no rechazar la hipótesis nula y valores p>0.05 --- ## Correciones a problemas de Heterocedasticidad. - estimar un modelo de regresión con errores estándar robustos a heterocedasticidad (Ej: Errores Estándar Robustos de White). En R: ```r library(lmtest) library(sandwich) model_robust<- coeftest(model, vcov=vcovHC) ``` - luego, comparar ambos modelos --- class: inverse middle ## **A revisar:** .pull-left-wide[ 1. Observaciones influyentes 2. Linealidad 3. Homogeneidad de varianza (homocedasticidad) 4. **Inflación de varianza** ] .pull-right-narrow[ <br> <br> <br>  ] --- ## Multicolinealidad / inflación de varianza de error - un supuesto de los modelos de regresión es que los predictores no están (altamente) correlacionados - en casos de alta correlación, se produce una inflación de los errores estándar, disminuyendo los valores t y afectando el rechazo de la hipótesis nula --- ## Detección: VIF `$$VIF=\frac{1}{1-R^{2}_x}$$` - VIF (Variance Inflation Factor): se calcula en base a un modelo donde `\(X\)` es la dependiente y las otras X independientes. - Mientras mayor el `\(R^2_x\)`, más pequeño el denominador y mayor será VIF, indicando alta multicolinealidad para esa variable --- ## Interpretación del VIF - Si `\(VIF=1\)`, entonces `\(R^{2}_x=0\)`, queriendo decir que la variable open es completamente independiente de las otras variables explicativas del modelo original. - Sin embargo, si `\(VIF=10\)`, entonces `\(R^{2}_x=0.9\)`, queriendo decir que el 90% de la varianza de la variable open puede ser explicada por las otras variables explicativas del modelo. --- ## Estimación de VIF Para análizar el supuesto de no multicolinealidad en R, usamos la función **vif** de la librería car. ```r car::vif(model1) ``` - valores mayores a 2.5 pueden indicar alta multicolinealidad --- class: inverse ## Resumen .pull-left-narrow[ <br> <br> <br>  ] .pull-right[ 1. Observaciones influyentes 2. Linealidad 3. Homogeneidad de varianza (homocedasticidad) 4. Inflación de varianza ] --- class: inverse ## Recomendaciones generales - buenos descriptivos uni y bivariados - informar procedimientos y decisiones --- class: roja ## Próximo bloque: pendientes varios breves - estandarización - casos perdidos --- class: front .pull-left[ # Estadística Multivariada ## Juan Carlos Castillo ## Sociología FACSO - UChile ## 1er Sem 2022 ## [multivariada.netlify.com](https://multivariada.netlify.com) ] .pull-right[ .right[ <br>  ] ] --- class: front .pull-left[ # Estadística Multivariada ## Juan Carlos Castillo ## Sociología FACSO - UChile ## 1er Sem 2022 ## [multivariada.netlify.com](https://multivariada.netlify.com) ] .pull-right[ .right[  <br> <br> <br> ## Sesión 10. Segundo bloque: Valores perdidos y estandarización ] ] --- layout: true class: animated, fadeIn --- ## Valores perdidos - la proporción de valores perdidos no es trivial para la estimación, principalmente si estos perdidos no son aleatorios - atender siempre al N de los modelos, no debería presentar una proporción de perdidos > 30% (app) - ante alta proporción de valores perdidos, análizar causas e intentar rescatar la mayor cantidad de casos posibles --- ## Rescatando valores perdidos: variable dependiente - descriptivos y cruces, buscar el origen de los perdidos -- - descartar posibles preguntas filtro en el instrumento -- - evaluar si cambiar de base de datos -- - evaluar alternativa a OLS que permita integrar perdidos como categoría luego de transformación (ej: regresión logistica multinomial) --- ## Rescatando valores perdidos: variable(s) independiente(s) - establecer origen de la pérdida de datos - procedimientos de imputación (avanzado) - alternativa simple: transformar a categórica e incluir un nivel/categoría de perdidos --- ## Rescatando perdidos: ingreso - caso típico de presencia de valores perdidos - pasar a categorías (ej: deciles/quintiles) y agregar categoría con missings - Detalles en [Práctica 11](https://multivariada.netlify.app/assignment/11-code/#recuperar-casos-perdidos-1) --- ## Ejemplo: variable autoubicación izquierda-derecha Datos ELSOC 2016 .tiny[ ``` ## Autoubicacion escala izquierda-derecha (x) <numeric> ## # total N=2927 valid N=2927 mean=-13.20 sd=139.05 ## ## Value | Label | N | Raw % | Valid % | Cum. % ## -------------------------------------------------------------------- ## -999 | No Responde (no leer) | 23 | 0.79 | 0.79 | 0.79 ## -888 | No Sabe (no leer) | 43 | 1.47 | 1.47 | 2.25 ## 0 | 0 Izquierda | 122 | 4.17 | 4.17 | 6.42 ## 1 | 1 | 58 | 1.98 | 1.98 | 8.40 ## 2 | 2 | 111 | 3.79 | 3.79 | 12.20 ## 3 | 3 | 135 | 4.61 | 4.61 | 16.81 ## 4 | 4 | 157 | 5.36 | 5.36 | 22.17 ## 5 | 5 Centro | 604 | 20.64 | 20.64 | 42.81 ## 6 | 6 | 98 | 3.35 | 3.35 | 46.16 ## 7 | 7 | 94 | 3.21 | 3.21 | 49.37 ## 8 | 8 | 84 | 2.87 | 2.87 | 52.24 ## 9 | 9 | 23 | 0.79 | 0.79 | 53.02 ## 10 | 10 Derecha | 110 | 3.76 | 3.76 | 56.78 ## 11 | 11 Independiente (no leer) | 200 | 6.83 | 6.83 | 63.61 ## 12 | 12 Ninguno (no leer) | 1065 | 36.39 | 36.39 | 100.00 ## <NA> | <NA> | 0 | 0.00 | <NA> | <NA> ``` ] --- ## Ejemplo: variable autoubicación izquierda-derecha - Definir categorías, ejemplo: Ninguno, Izquierda, Centro, Derecha, Independiente - Decidir sobre valores que se asocian a cada categoría - Recodificar - Re-etiquetar --- ## Ejemplo: variable autoubicación izquierda-derecha .medium[ ```r # Recodificar elsoc_2016$c15_cat <- car::recode(elsoc_2016$c15, "c(-888,-999,12)=1; c(0,1,2,3)=2; c(4,5,6)=3; c(7,8,9,10)=4; 11=5") # Re-etiquetar elsoc_2016$c15_cat <- set_labels(elsoc_2016$c15_cat, labels= c("Ninguno"=1, "Izquierda"=2, "Centro"=3, "Derecha"=4, "Independiente"=5)) ``` ] --- ## Ejemplo: variable autoubicación izquierda-derecha .medium[ ```r frq(elsoc_2016$c15_cat) ``` ``` ## Autoubicacion escala izquierda-derecha (x) <numeric> ## # total N=2927 valid N=2927 mean=2.32 sd=1.27 ## ## Value | Label | N | Raw % | Valid % | Cum. % ## ------------------------------------------------------- ## 1 | Ninguno | 1131 | 38.64 | 38.64 | 38.64 ## 2 | Izquierda | 426 | 14.55 | 14.55 | 53.19 ## 3 | Centro | 859 | 29.35 | 29.35 | 82.54 ## 4 | Derecha | 311 | 10.63 | 10.63 | 93.17 ## 5 | Independiente | 200 | 6.83 | 6.83 | 100.00 ## <NA> | <NA> | 0 | 0.00 | <NA> | <NA> ``` ] --- # Estandarización ## ¿Qué coeficiente es mayor que otro? - usualmente, los coeficientes se encuentran en escalas diferentes - para poder comparar la magnitud de un coeficiente en relación a los otros se requiere pasar a una escala común - esto se efectúa mediante el proceso de **estandarización** --- ## Estandarización de Coeficientes - Para poder expresar las variables en escalas comparables, sus valores se ponderan respecto de su desviación estándar. - Para ello, a cada valor de la variable se le resta el promedio y se divide por su desviación estándar, lo que se conoce como **puntaje Z**: `$$z_x=\frac{x-\bar{x}}{sd(x)}$$` - Este procedimiento se aplica tanto a la dependiente como a las independientes --- ## Estandarización: interpretación - al estandarizar, los coeficientes de regresión reflejan cuantas **desviaciones estándar** cambia _Y_ como consecuencia del cambio en **una desviación estándar** _X_. - los coeficientes ahora son comparables entre sí en base a su magnitud --- ## Estandarización de Coeficientes De la [Práctica 6 - regresión multiple 2](https://multivariada.netlify.app/assignment/06-code/): - *colGPA*: promedio general de calificaciones de la universidad, en escala de 0 a 4 puntos. - *hsGPA*: promedio general de calificaciones en la enseñanza media, en escala de 0 a 4 puntos - *ACT* : puntaje en el examen de admisión a la universidad, que va de 16 a 33 puntos --- ## Estandarización de Coeficientes Función `scale` ```r library(wooldridge) data('gpa1') # Cargar base de datos gpa1 <- dplyr::select(gpa1, colGPA, hsGPA, ACT) col_model <- lm(colGPA ~ ACT + hsGPA, data = gpa1) gpa1_std = data.frame(scale(gpa1)) col_model_std <- lm(colGPA ~ ACT + hsGPA, data = gpa1_std) ``` --- ## Estandarización de Coeficientes .center[  ] --- ## Estandarización de Coeficientes En este caso se puede observar que por el aumento en **una desviación estándar** en las calificaciones de enseñanza media (hsGPA), el promedio de notas en la universidad (colGPA) aumenta **0.39 desviaciones estándar**. Al estar en una misma unidad de medida, podemos comparar los coeficientes en términos de su tamaño. --- class: front .pull-left[ # Estadística Multivariada ## Juan Carlos Castillo ## Sociología FACSO - UChile ## 1er Sem 2022 ## [multivariada.netlify.com](https://multivariada.netlify.com) ] .pull-right[ .right[ <br>  ] ]