Práctica 4. Regresión simple 2
Índice
Objetivo de la práctica
En esta guía práctica revisaremos un ejemplo que fue presentado en la clase de Regresión Simple 2, se recomienda revisar el documento de presentación antes de realizar esta guía.
La idea es volver sobre el cálculo e interpretación de los coeficientes del modelo de regresión paso a paso y de la forma más manual posible, de modo de poder familiarizarse más cercanamente con el sentido de esta técnica y también para darse cuenta que lo que se obtendrá luego con el análisis en R no es magia sino que proviene de un procedimiento que se puede realizar también mediante lápiz y papel … o también con ayuda de una planilla simple de cálculo. Para ello usaremos un ejemplo con solo cuatro casos a modo ilustrativo.
Además, vamos a revisar el cálculo e interpretación de \(R^2\) que es una medida de qué tan bien se ajusta el modelo de regresión a los datos. En otras palabras, qué tan bueno es el modelo, o cuánto de nuestra variable dependiente \(Y\) podemos saber/predecir a partir de nuestra variable independiente \(X\).
Librerías
pacman::p_load(stargazer, ggplot2, dplyr, webshot, sjPlot)Datos
Del ejemplo de la sesión de Regresión Simple 2 recordemos que el objetivo del ejercicio es poder predecir cuántos pasos da un hij_ por cada paso que da su madre. Tomemos como supuesto que l_s niñ_s son de la misma edad, y que se midieron los pasos de ambos mientras caminaban juntos. Entonces,la pregunta es: ¿Cuántos pasos da un hij_ (Y) por cada paso que da su mamá (X)? En otras palabras, ¿puedo predecir cuantos pasos da un niñ_ si sé cuantos pasos ha dado su mamá?
Para esto vamos a generar un set de datos ficticios datos1:
pasos_mama_x=c(3,5,7,9)
pasos_hijo_y=c(2,3,2,4)
datos1 <-as.data.frame(cbind(pasos_hijo_y, pasos_mama_x))
datos1## pasos_hijo_y pasos_mama_x
## 1 2 3
## 2 3 5
## 3 2 7
## 4 4 9Tenemos una base de datos con cuatro casos y dos variables: pasos_hijo_y y pasos_mama_x. Una representación en un gráfico bivariado de puntos es la siguiente:

Vemos la distribución de los cuatro casos, se aprecia en general una relación positiva donde a medida que aumentan los pasos de la madre también aumenta la cantidad de pasos de los hij_s.
Cálculo de los coeficientes de regresión
Recordemos la ecuación del modelo de regresión:
\(\hat{Y}= \beta_0 + \beta_{1}X_{1}\)
En esta sección vamos a calcular un modelo de regresión para las variables de datos1, siendo pasos_hijo_y nuestra variable dependiente \(Y\), y pasos_mama_x nuestra variable independiente \(X\). Recordemos la fórmula del beta ( \(\beta\) ) de regresión:
\[b_{1}=\frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})} {\sum_{i=1}^{n}(x_i - \bar{x})(x_i - \bar{x})}\]
En el numerador (parte superior de la fracción) tenemos lo que se llama suma de productos cruzados, que representa la covariación entre \(X\) e \(Y\), y abajo la suma de los cuadrados de x, que representa la variación (varianza) de \(X\). El sentido de esta formula es llegar a un número que represente cuánto cambia \(Y\) por cada punto o unidad que aumenta \(X\).
Este calculo lo vamos a hacer usando una planilla de cálculo, para ellos se puede usar Excel, Drive, o una hoja y un lápiz. Se recomienda hacerlo paso a paso siguiendo las indicaciones que vienen a continuación.

En la tabla aparecen nuestras variables \(Y\) y \(X\) en las columnas B y C respectivamente, bajo ellas se calcula la suma y el promedio de cada variable. Para poder calcular el \(\beta\) necesitamos obtener cada término de la formula, que finalmente no son más que diferencias de cada caso respecto de su promedio, y luego la suma de ellos. Vamos por parte.
agregamos en la columna D y-promy, que es el caso correspondiente de \(Y\) (pasos hijo) menos su promedio. Por ejemplo, el primer caso de \(Y\) tiene el valor 2, y su promedio es 2,75. Por lo tanto, 2-2,75=-0.75, que es el valor a anotar en la celda correspondiente (columna D de la fila del caso 1).
luego, en la columna x-promx se hace lo mismo pero para la variable \(X\) pasos_mama_x
en la columna siguiente (x-promx)2 se eleva al cuadrado el valor de la columna anterior para cada caso, y al final se suman. Esto corresponde al denominador del \(\beta\) (lo que va en la parte de abajo de la fracción= \(\sum_{i=1}^{n}(x_i - \bar{x})(x_i - \bar{x})\) )
y en la columna siguiente multiplicamos x-promx por y-promy para cada caso y lo sumamos al final, que corresponde al numerador de la fracción del beta= \(\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})\)
El resultado de estos cálculos se puede ver acá:
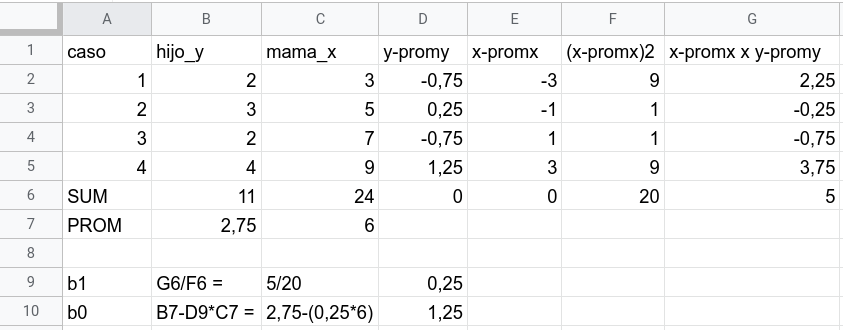
En la parte de abajo se incluye el cálculo del \(\beta\) o más precisamente el \(\b_1\), que es el que corresponde a la (primera) variable independiente X, pasos_mama_x. Este beta se obtiene dividiendo la celda G6 ( \(\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})\) ) por la celda F6 ( \(\sum_{i=1}^{n}(x_i - \bar{x})(x_i - \bar{x})\) ), y nos da un resultado de 0,25. **Este es el valor del \(\beta\) de regresión para esta ecuación.
Para el cálculo del intercepto de la ecuación o \(\beta_0\) aplicamos la siguiente fórmula:
\[b_{0}=\bar{Y}-b_{1}\bar{X}\]
Que corresponde al promedio de \(Y\) (2,75) menos el \(\beta_1\) 0,25 por el promedio de \(X\) (6), lo que nos da 1,25.
Con esto podemos completar nuestra ecuación de regresión:
\[\widehat{Y}=1.25 +0.25X\]
Entonces:
interpretación del \(\beta\) : por cada paso que da la mamá (\(X\)), un hij_ (\(Y\)) avanza en promedio 0.25 pasos
uso en predicción: si una mamá da (por ej) 4 pasos, entonces la cantidad de pasos estimada para su hijo sería 1.25+0.25*4=2.25
La ecuación de regresión se puede representar en una recta, donde cada valor de la recta corresponde al valor predicho de \(Y\) para cada valor de \(X\):

Ajuste y residuos
En el gráfico anterior vemos la línea que representa la relación entre \(X\) e \(Y\) que se denomina recta de regresión, caracterizada por un intercepto (valor de \(Y\) cuando \(X\) es cero) y una pendiente o \(\beta\). Claramente, esta recta es una simplificación que no abarca toda la variabilidad de los datos y por lo tanto se generará una diferencia entre los valores observados de \(Y\) y los valores predichos por el modelo que aparecen en la recta de regresión. Esta diferencia entre predicho (\(\widehat{Y}\)) y observado (\(Y\)) es lo que se conoce como residuo.
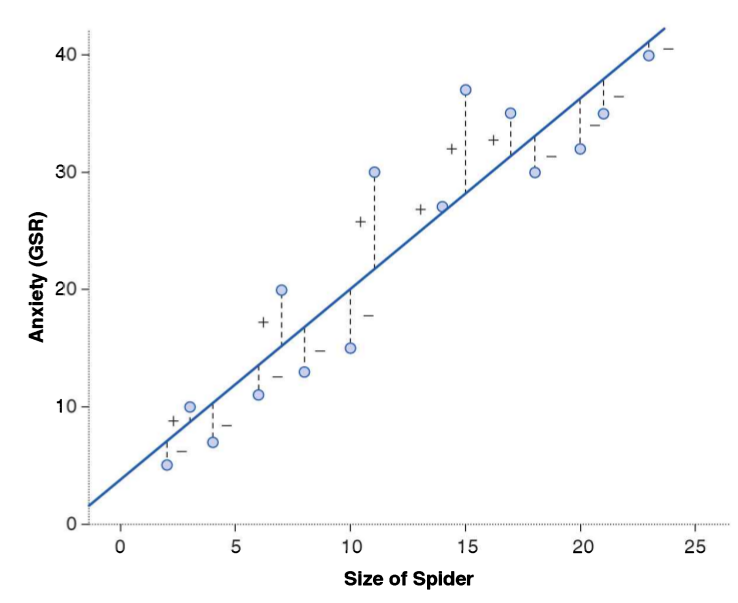
En la imagen, los circulos corresponden a los valores observados, y lo que está en la recta son los valores predichos. La línea punteada entre ambos representa el residuo.
Los residuos ayudan en primer lugar a entender el sentido del cálculo de la recta de regresión. La mejor recta será aquella que minimice lo más posible el valor de los residuos. Para realizar la suma de los residuos estos se elevan al cuadrado, lo que se denomina suma de residuos al cuadrado o \(SS_{residual}\) (ya que como hay residuos positivos y negativos unos se cancelan a otros y la suma es 0). Por lo tanto, el cálculo de la recta de regresión busca que la suma de todos los residuos (al cuadrado) sea la menor posible, que es justamente lo que hicimos arriba con la fórmula del \(\beta\). Este procedimiento es el que da nombre al proceso de estimación: minimos cuadrados ordinarios, o OLS (Ordinary Least Squares).
Ahora, considerando que un mismo modelo de regresión puede representar distintas distribuciones de datos con distintos residuos (ver cuarteto de Anscombe en la sesión Regresión Simple 2, pag. 23), se requiere información adicional para poder evaluar qué tan bueno es el modelo, lo que se conoce como bondad de ajuste. La pregunta es: ¿qué tan bien representa mi modelo a la distribución de los datos? ¿Me permite hacer una buena predicción de Y a partir de X, o mi predicción no es tan buena? Una forma de evaluar esto es calcular la cantidad de residuos que genera el modelo. Sin embargo, si sumamos los residuos nos quedamos con un número difícil de interpretar en términos de ajuste. Por ello, el ajuste se representa en un número sencillo que es el \(R^2\).
El \(R^2\) es un número que varía entre 0 y 1 y que representa qué porcentaje de la varianza de \(Y\) podemos explicar con \(X\). A menores residuos, mejor predicción, y entonces mayor \(R^2\). De otra manera, si todos los valores predichos calzaran perfecto en la recta de regresión tendríamos cero residuos, y por lo tanto el \(R^2\) sería 1.
Cálculo del R2
Se puede representar de la siguiente manera:
\[R^2=\frac{SS_{reg}}{SS_{tot}}\]
- El primer término \(SS_{reg}\) es la Suma de cuadrados de la regresión, y representa la diferencia entre lo estimado (\(\hat{y}\)) y el promedio de Y ( \(\bar{y}\)). Se puede interpretar como cuánto de Y podemos conocer (además de su promedio) si es que también conocemos X. En otras palabras: ¿cuánto me aporta \(X\) para saber de \(Y\), más allá del mero promedio de \(Y\)? Para ello, se resta a lo estimado el promedio de Y para cada caso, y luego se suma:
\[SS_{reg} = \sum(\hat{y}-\bar{y})^2\]
- Suma Total de Cuadrados ( \(SS_{tot}\) ) : La suma de las diferencias del promedio de Y al cuadrado (que representa la varianza total de Y)
\[SS_{tot} = \sum(y-\bar{y})^2 \]
Para ejemplificar el cálculo vamos a seguir con la misma planilla que usamos para calcular los parámetros del modelo de regresión, agregando las siguientes columnas:
predY: predicción de \(Y\) (pasos hijo) a partir de nuestro modelo de regresión
predY-promY : la predicción de \(Y\) - su promedio
(predY-promY)2: se eleva cada valor al cuadrado; la suma de esto nos da \(SS_{reg}\)
y-promy2: las diferencias de cada valor de \(Y\) de su promedio (que ya estaban en la columna D) al cuadrado. La suma de esto nos da \(SS_{tot}\)

Reemplazando,
\[R^2=\frac{SS_{reg}}{SS_{tot}}=\frac{1,25}{2,75}=0,455\]
Entonces, el porcentaje de varianza de nuestra variable dependiente \(Y\) “pasos_hijo_y” que podemos relacionar con nuestra variable independente X “pasos_mama_x” es de un 45%. En otras palabras, si conocemos los pasos de la madre podemos explicar/conocer un 45% de los pasos de los hijos. Y de otra manera, hay un 55% de la varianza de \(Y\) que no se asocia a \(X\) … y que probablemente tiene que ver con otras variables.
Vamos a R
Cálculo del modelo de regresión:
modelo1 <- lm(pasos_hijo_y ~ pasos_mama_x, data = datos1)Como vimos la práctica anterior, aplicamos la funcion lm (linear model) y obtenemos los parámetros correspondientes que podemos visualizar así:
summary(modelo1)##
## Call:
## lm(formula = pasos_hijo_y ~ pasos_mama_x, data = datos1)
##
## Residuals:
## 1 2 3 4
## 0.0 0.5 -1.0 0.5
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.2500 1.2400 1.008 0.420
## pasos_mama_x 0.2500 0.1936 1.291 0.326
##
## Residual standard error: 0.866 on 2 degrees of freedom
## Multiple R-squared: 0.4545, Adjusted R-squared: 0.1818
## F-statistic: 1.667 on 1 and 2 DF, p-value: 0.3258Esta tabla es algo rudimentaria y entrega más información de la que podemos interpretar hasta ahora, pero lo importante es que en la columna “Estimate” aparece el cálculo de los parámetros del intercepto (1,25) y del beta de regresión correspondiente a la variable \(X\) pasos_mama_x (0,25). Además, abajo en la leyenda aparece “Multiple R-squared”, que corresponde al \(R^2\) que calculamos arriba.
Una tabla con un mejor formato se puede visualizar con el comando tab_model, de la librería sjPlot. Nuevamente, aparece más información de la que podemos interpretar, lo importante es por ahora fijarse en la columna Estimates y en el \(R^2\)
sjPlot::tab_model(modelo1)| pasos hijo y | |||
|---|---|---|---|
| Predictors | Estimates | CI | p |
| (Intercept) | 1.25 | -4.09 – 6.59 | 0.420 |
| pasos_mama_x | 0.25 | -0.58 – 1.08 | 0.326 |
| Observations | 4 | ||
| R2 / R2 adjusted | 0.455 / 0.182 | ||
Correlación y regresión
Siguiendo con el ejemplo, la correlación entre las variables dependiente e independiente del ejemplo con datos1 es la siguiente:
cor(datos1$pasos_hijo_y, datos1$pasos_mama_x)## [1] 0.6741999Si elevamos este valor al cuadrado
(0.674)^2## [1] 0.454276… que es el valor que habíamos calculado para \(R^2\). Es decir, en este caso particular de regresión simple (una variable independiente \(X\)) \(r\) de Pearson al cuadrado es = \(R^2\), y nos dice qué parte de la varianza es compartida entre \(X\) e \(Y\).
Si bien hay similitudes entre correlación y regresión en términos de varianza compartida, también hay diferencias. La correlación es conmutativa, es decir, el orden de los factores no altera el producto:
cor(datos1$pasos_hijo_y, datos1$pasos_mama_x)## [1] 0.6741999cor(datos1$pasos_mama_x, datos1$pasos_hijo_y)## [1] 0.6741999Sin embargo, la regresión entre \(X\) e \(Y\) no es la misma que entre \(Y\) y \(X\):
lm(datos1$pasos_hijo_y ~ datos1$pasos_mama_x)$coefficients## (Intercept) datos1$pasos_mama_x
## 1.25 0.25lm(datos1$pasos_mama_x ~ datos1$pasos_hijo_y)$coefficients## (Intercept) datos1$pasos_hijo_y
## 1.000000 1.818182Esto se produce porque con la regresión se predice el valor de \(Y\) a partir de \(X\), y los valores de \(X\) son distintos en los dos casos.
Reporte de progreso
Completar el reporte de progreso aquí.